Knoten 1:
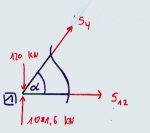
	Fx=0: S4 * cos(53,13°) + S12 = 0 <=> S12 = -S4 * cos(53,13°) => S12 = 721,20 kN (Z)	Fz=0: -S4 * sin(53,13°) - 120 + 1081,6 = 0 S4 = (120 - 1081,6) / sin(53,13°) => S4 = -1202,00 kN (D)
Knoten 2:
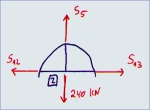
	Fx=0: -S12 + S13 = 0 <=> S12=S13 =>S13 = 721,20 kN (Z)	Σ Fz=0:240 - S5 = 0 => S5 = 240 kN (Z)
Knoten 10:
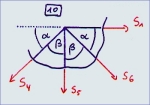
	Fx=0: -S4*cos(53,13°) + S6*cos(53,13°) + S1 = 0 <=> S1 = (S4 - S6)*cos(53,13°) => S1 = -1262,40 kN (D)	Fz=0: S4*sin(53,13°) + S6*sin(53,13°) + S5 = 0 <=> S6 = (-S5 - S6*sin(53,13°)) / sin(53,13°) => S6 = 902,00 kN (Z)
Knoten 11:
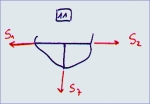
	Fx=0: -S1 + S2 = 0 <=>S1 = S2 => S2 = -1262,40 kN (Z)	Fz=0: S7 = 0
Knoten 3:
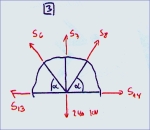
	Fx=0: -S13 - S6*cos(53,13°) + S8*cos(53,13°) + S14 = 0 <=> S14 = S13 + S6*cos(53,13°) - S8*cos(53,13°) => S14 = 1623,60 kN (Z)	Fz=0: -S6*sin(53,13°) - S7 - S8*sin(53,13°) + 240 = 0 <=> S8 = (-S6*sin(53,13°) + 240) / sin(53,13°) => S8 = -602,00 kN (D)
Knoten 4:
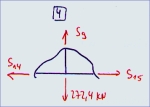
	Fx=0: S14 - S15 = 0 <=>S14 = S15 => S15 = 1623,60 kN (Z)	Fz=0: S9 = 272,4 kN
Knoten 12:
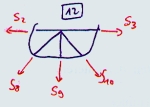
	Fx=0: -S2 - S8*cos(53,13°) + S10*cos(53,13°) + S3 = 0 <=> S3 = S2 + S8*cos(53,13°) - S10*cos(53,13°) => S3 = -1780,50 kN (D)	Fz=0: S8*sin(53,13°) + S9 + S10*sin(53,13°) = 0 <=> S10 = ( -S9 - S8*sin(53,13°) / sin(53,13°) => S10 = 261,50 kN (Z)

(D) = Druckstab (Z) = Zugstab

Die verbleibenden Kräfte S16 bis S19 folgen aus der Symmetrie.

Verprobung:
Durch einen Ritterschnitt durch die Stäbe 3/10/15 ergbibt sich aus Momentengleichgweicht ebenfalls die Stabkraft S3 zu -1780,50 kN, was zeigt, dass wir uns nicht verrechnet haben.