Zur Homepage von
Jörg Winkelmann
Zur Homepage zur
Vorlesung
Mathematisches Institut der Universität Basel
Vorlesung Infinitesimalrechnung I (WS 99/00)
PD Dr. Jörg Winkelmann
Abgabetermin: 7. April 2000
- 1.
- Zeige:
Das Legendre-Polynom Pn
(siehe
Aufgabenblatt 13)
genügt der Differentialgleichung
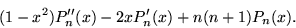
- 2.
- Man untersuche die durch f(x)= x3+ax2+bx gegebene Funktion
auf lokale Extrema in Abhängigkeit von den Parametern
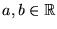 .
.
- 3.
- Man bestimme eine Rekursionsformal für die Integrale
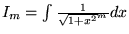 .
.
- 4.
- Unter Verwendung von Aufgabe 6* von Blatt 13 zeige man:
Es gibt eine auf ganz
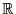 unendlich oft differenzierbare Funktion
f mit
unendlich oft differenzierbare Funktion
f mit
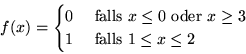
- 5.
- Sei
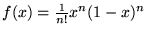 .
Zeige: Für alle
.
Zeige: Für alle 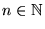 und
und 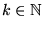 gilt
gilt 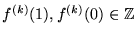 .
.
- 6.
- Sei
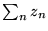 eine komplexe Reihe, die nicht absolut konvergent ist.
eine komplexe Reihe, die nicht absolut konvergent ist.
Zeige: Es gibt eine divergente Umordnung, also eine Bijektion
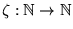 sodass
sodass 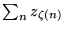 divergiert.
divergiert.
- 7.
- Sei
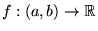 stetig und
stetig und 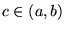 ,
sodass
f in allen Punkten
,
sodass
f in allen Punkten 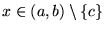 differenzierbar
ist. Man nehme darüberhinaus an, dass
differenzierbar
ist. Man nehme darüberhinaus an, dass 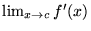 existiert.
existiert.
Zeige:
Dann ist f in c differenzierbar und es gilt 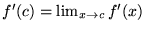
Joerg Winkelmann
2000-02-11
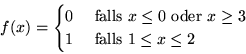
![]() sodass
sodass ![]() divergiert.
divergiert.
![]()
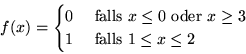
![]() sodass
sodass ![]() divergiert.
divergiert.
![]()