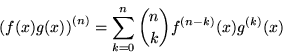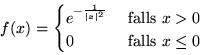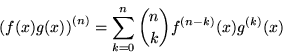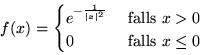Zur Homepage von
Jörg Winkelmann
Zur Homepage zur
Vorlesung
Mathematisches Institut der Universität Basel
Vorlesung Infinitesimalrechnung I (WS 99/00)
PD Dr. Jörg Winkelmann
Abgabetermin: 4. Februar 2000
- 1.
- Sei
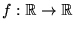 eine konvexe Funktion.
Zeigen Sie: f ist stetig.
eine konvexe Funktion.
Zeigen Sie: f ist stetig.
- 2.
- Eine Funktion
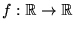 heißt ``gerade'' falls
heißt ``gerade'' falls
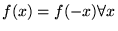 und ``ungerade'' falls
und ``ungerade'' falls
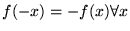 .
.
- (a)
- Zeigen Sie:
Die Ableitung einer geraden Funktion ist ungerade.
- (b)
- Ein Polynom
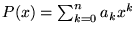 ist genau dann
gerade wenn ak=0 für alle ungeraden k .
ist genau dann
gerade wenn ak=0 für alle ungeraden k .
- 3.
- Die ``Legendre-Polynome'' sind wie folgt definiert:
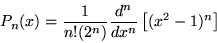 Zeige Sie, dass für jedes
Zeige Sie, dass für jedes 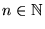 das Legendre-Polynom Pn genau
n paarweise verschiedene Nullstellen im Intervall ]-1,1[
besitzt.
das Legendre-Polynom Pn genau
n paarweise verschiedene Nullstellen im Intervall ]-1,1[
besitzt.
- 4.
- Berechne
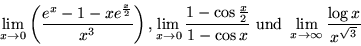
- 5.
- Sei
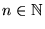 und f eine n -mal differenzierbare Funktion auf
und f eine n -mal differenzierbare Funktion auf 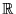 .
Beweise folgende ``Leibnitzregel'' für höhere Ableitungen
(wobei f(k) die k -te Ableitung von f bezeichnet
mit f(0)=f ):
.
Beweise folgende ``Leibnitzregel'' für höhere Ableitungen
(wobei f(k) die k -te Ableitung von f bezeichnet
mit f(0)=f ):
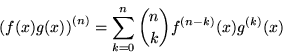
- (*) 6.
- Sei
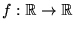 gegeben durch
gegeben durch
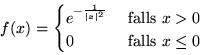
Zeigen Sie, dass f unendlich oft differenzierbar ist.
Joerg Winkelmann
2000-02-01
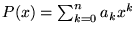 ist genau dann
gerade wenn ak=0 für alle ungeraden k .
ist genau dann
gerade wenn ak=0 für alle ungeraden k .