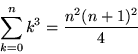Zur Homepage von
Jörg Winkelmann
Zur Homepage zur
Vorlesung
Mathematisches Institut der Universität Basel
Vorlesung Infinitesimalrechnung I (WS 99/00)
PD Dr. Jörg Winkelmann
Abgabetermin: 7. Januar 2000
- 1.
- Sei a0=1 ,
 Bestimme
Bestimme 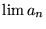 .
.
- 2.
- Zeige:
Es gibt Folgen an , bn , An , Bn ,
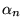 ,
,
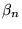 in
in 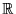 mit
mit
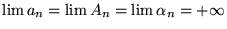 und
und 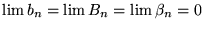 ,
sodass
,
sodass
- 3.
- Zeige:
- (a)
- Sei zn eine Folge in
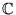 mit
mit 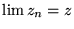 .
Dann gilt
.
Dann gilt
 .
.
- (b)
- Für alle
 gilt:
gilt: 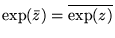 .
.
- (c)
- Für alle
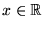 gilt: |eix|=1 .
gilt: |eix|=1 .
- 4.
- Die Funktionen
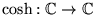 und
und 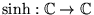 sind definiert
durch
sind definiert
durch
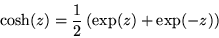 und
und
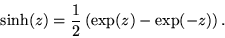 Zeige:
Es gilt:
Zeige:
Es gilt:
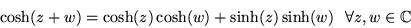 und
und
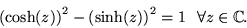
- 5.
- Sei
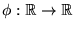 definiert durch
definiert durch 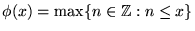 und
und 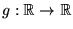 durch
durch 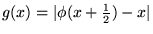 .
.
Welche der Abbildungen  und g sind stetig?
und g sind stetig?
- (*) 6.
- Sei
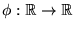 definiert wie in Aufgabe 5.
Sei
definiert wie in Aufgabe 5.
Sei 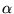 eine irrationale reelle Zahl.
Zeige:
eine irrationale reelle Zahl.
Zeige:
Jede Zahl im abgeschlossenen Intervall [0,1] ist Häufungspunkt
der Folge 
- (*) 7.
- Sei K ein endlicher Körper.
Zeige:
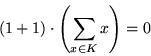
- W1.
- Zeige:
Für
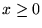 ,
,
 gilt:
gilt:
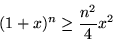
- W2.
- Zeige:
Für alle
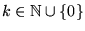 ,
,
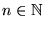 gilt:
gilt:
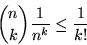
- W3.
- Zeige:
Für alle
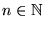 gilt:
gilt:
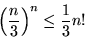
- W4.
- Zeige:
Für alle
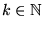 gilt:
gilt:
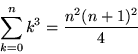
- W5
- Für
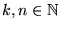 leite man eine Formel her, die angibt, wieviele
injektive Abbildungen von einer Menge mit k Elementen in eine
Menge mit n Elementen existieren.
leite man eine Formel her, die angibt, wieviele
injektive Abbildungen von einer Menge mit k Elementen in eine
Menge mit n Elementen existieren.
Die Aufgaben W1-W5 sind ``Weihnachts-'' oder ``Wiederholungsaufgaben''.
Sie werden wie (*) -Aufgaben gewertet, sind aber einfacher.
Dadurch soll es ermöglicht werden,
eventuelle Punkterückstande aufzuarbeiten.
Mindestpunktzahl für dieses Aufgabenblatt ist also
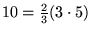 .
.
Joerg Winkelmann
2000-01-11
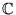 mit
mit 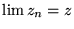 .
Dann gilt
.
Dann gilt
 .
.
 gilt:
gilt: 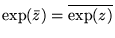 .
.
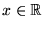 gilt: |eix|=1 .
gilt: |eix|=1 .
![]() und g sind stetig?
und g sind stetig?
![]()
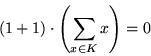
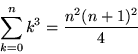
![]() und g sind stetig?
und g sind stetig?
![]()