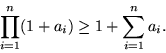Abgabetermin: 3. Dezember 1999
- 1.
- Für
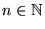 sei
sei
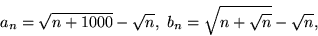
Zeige:
Für 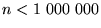 gilt
gilt 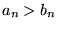 ,
aber
,
aber 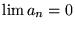 und
und 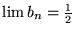 .
.
- 2.
- Die Folge (an) ist rekursiv definiert durch a1=1 und
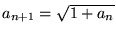 für
für 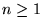 .
.
Konvergiert an und wenn ja, wogegen?
- 3.
- Seien
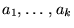 nichtnegative reelle Zahlen.
nichtnegative reelle Zahlen.
Zeige:
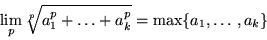
- 4.
- Seien
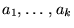 reelle Zahlen mit
reelle Zahlen mit  für
alle
für
alle 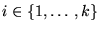 .
.
Man muss zusätzlich voraussetzen, dass all ai
dasselbe Vorzeichen haben.
Zeige:
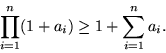
- 5.
- Sei
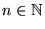 ,
A eine Menge mit n Elementen und B eine Menge
mit n+2 Elementen.
,
A eine Menge mit n Elementen und B eine Menge
mit n+2 Elementen.
Wieviele surjektive Abbildungen gibt es von B nach A ?
- (*) 6
- Die Folgen (an) und (bn) seien gegeben a1=a , b1=b
und
 für
für 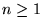 ,
wobei a und b feste reelle Zahlen mit
,
wobei a und b feste reelle Zahlen mit 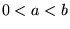 sind.
sind.
Zeigen Sie, dass (an) und
(bn) konvergieren und bestimmen Sie
die Grenzwerte.
![]() gilt
gilt ![]() ,
aber
,
aber ![]() und
und ![]() .
.
![]()