Vermessungskunde Übung 3

3. Sommerübung:

Inhaltsverzeichnis:

Poygonzug

3.1. Erläuterung der Aufgabenstellung in eigenen Worten 2

3.2. Beschreibung des Messverfahren 2

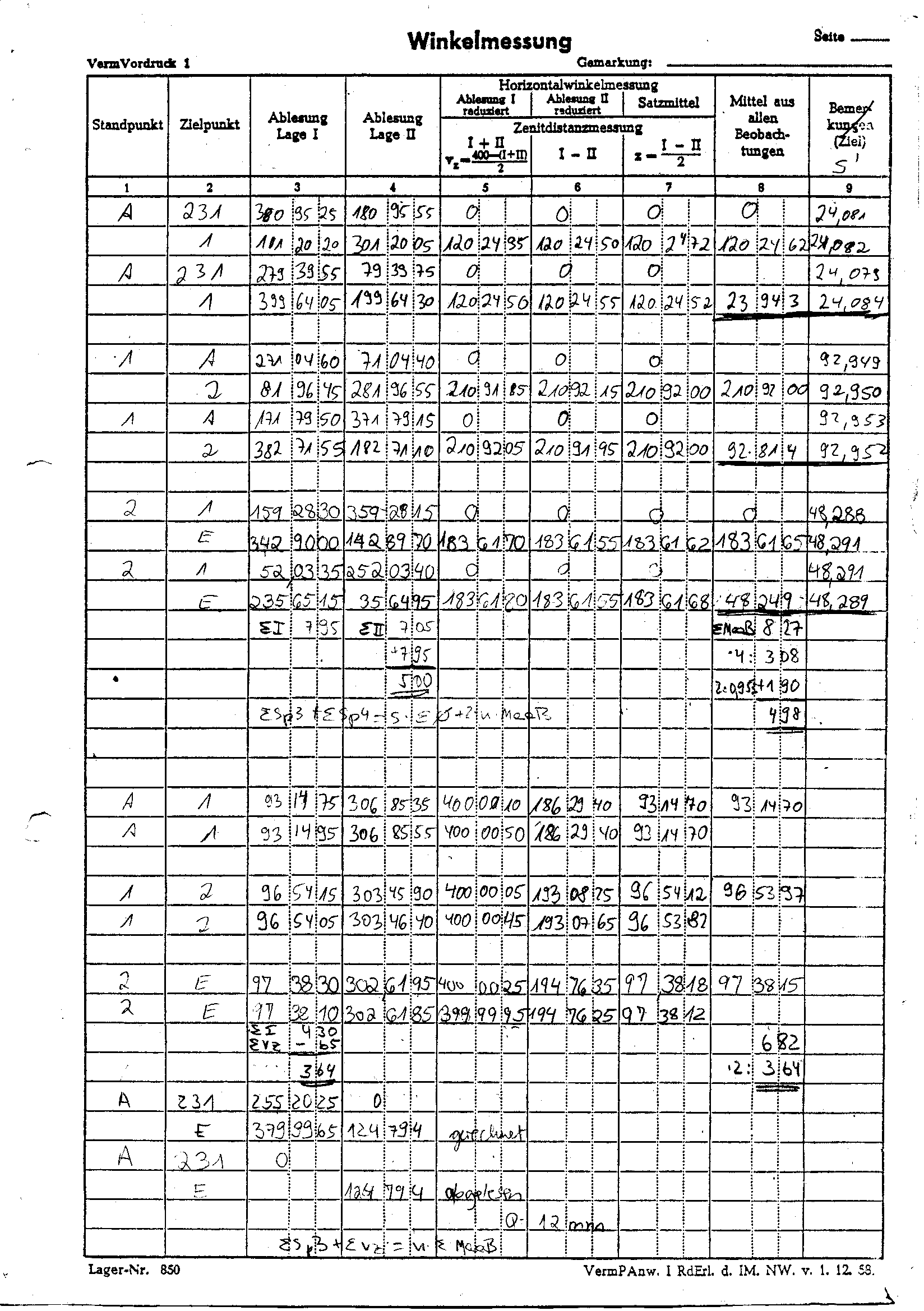
3.3.1. Messprotokoll "Winkel" mit Verprobung 3

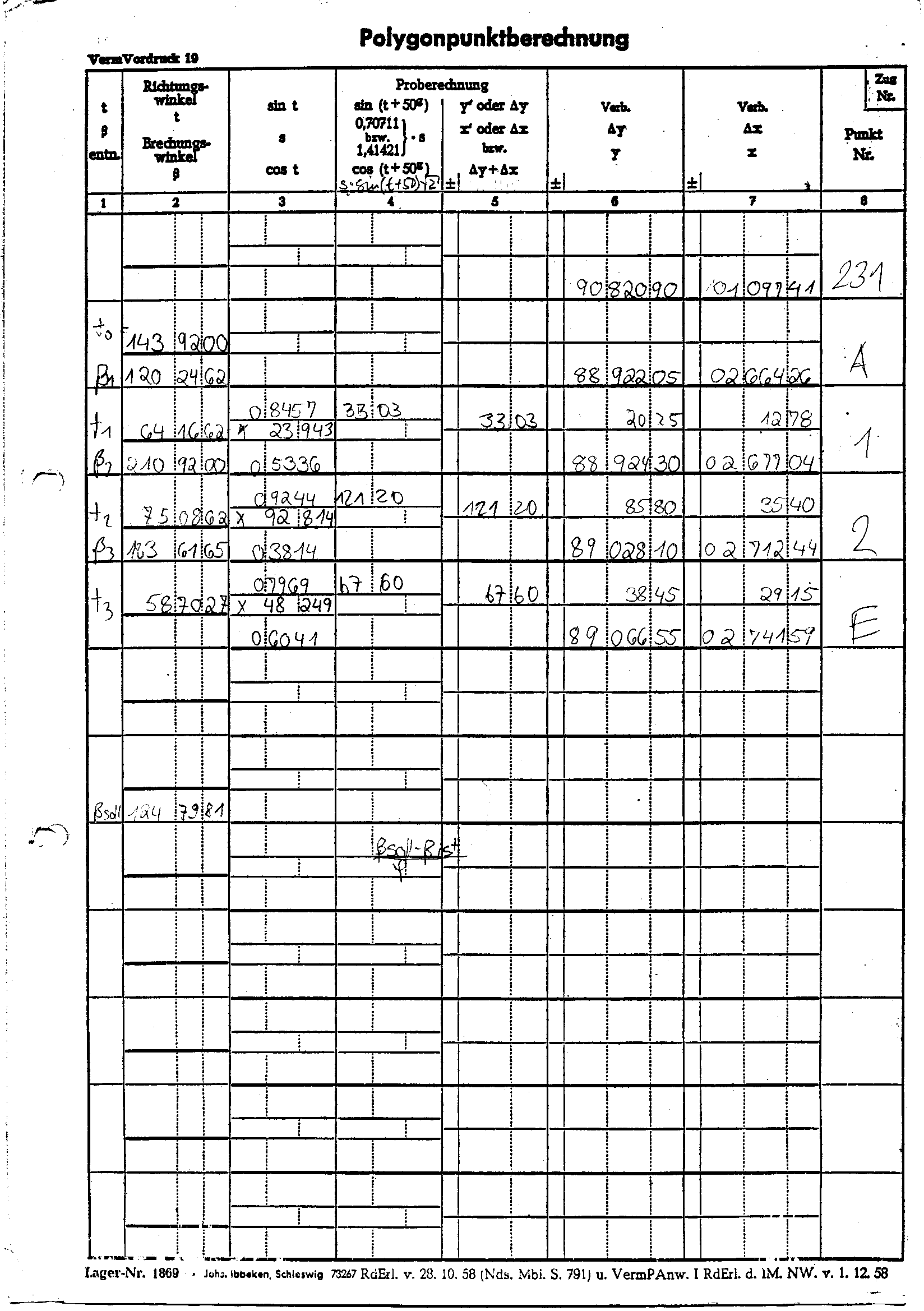
3.3.2. Messprotokoll "Poygonpunkt" mit Verprobung 4

3.4. Auswertung der Beobachtungsdaten 5

3.5. Statistik 5

3.6. Zusammenfassung der Ergebnisse und beurteilende Stellungnahme 7

3.7. Graphische Darstellung der zu erwartenden Abweichungen 8

3.1. Erläuterung der Aufgabenstellung in eigenen Worten

Mit Hilfe eines elektrooptischen Tachymeters soll die Richtung von Punkten A zu E bestimmt werden. Die direkte Verbindung ist dabei nicht sichtbar, so dass ein offener Polygonzug gemessen werden muss. Die Gauß-Krüger-Koordinaten des Punktes A und der Anschlussrichtung N sind bekannt. Mit dem offenen Polygonzug sollen die Koordinaten ds Punktes E bestimmt werden, sowie der Brechungswinkel b am Punkt A von N zu E.

Am Ende wird die Genauigkeit der Messung überprüft indem die Richtung von A aus anvisiert wird. Durch hochhalten eines Stabes wird dann die tatsächliche Richtung des Punktes B angezeigt.

3.2. Beschreibung des Messverfahren

Bei der Polygonzugmessung ist es notwendig, dass dieselben Polygonpunkte mit verschiedenen Geräten nacheinander besetzt werden. Um Ungenauigkeiten bei erneuerter Zentrierung zu vermeiden, verwendet man das Prinzip der Zwangszentrierung. Der Dreifuss oder Kugelkopf bleibt immer im Stativ während nacheinander die einzelnen Geräte (Tachymeter, Spiegelprisma und Zieltafel) eingesetzt werden.

Das Aufstellen der Stative erfolgt immer nach dem gleichen Prinzip.

Aufstellen des Statives (möglichst zentrisch über dem Punkt)
Grobzentrierung mit Fußschrauben und optischem Lot
Grobhorizontrierung mit Stativbeinen und Dosenlibelle
Feinzentrierung mit Fußschraube und Röhrenlibelle
Feinhorizontrierung durch verschieben auf dem Stativteller
Notfalls Wiederholung von 4 und 5

Nach dem alle 3 Stative (P A, P2 und P3) aufgestellt worden sind wird nun mit der Messung in A begonnen. In je zwei Vollsätzen werden die Richtungen und Zenitwinkel zum Anschlusspunkt und zum ersten Polygonpunkt gemessen. Aus der Differenz der Richtungswinkel ergibt sich der Brechunswinkel.

Für die Horizontalstrecke, wird die Schrägstrecke zum nächsten Punkt je dreimal gemessen und mit folgender Formel

Horizontalstrecke = Schrägstrecke * sin(Zenitwinkel)

ausgerechnet.

Für die weiteren Polygonpunkte wird der rückliegende Punkt mit einer Zieltafel ausgestattet, um ihn besser anvisieren zu können. Die Messungen werden dann nach obigen Muster fortgesetzt, bis von P3 aus der Endpunkt angezielt werden kann.

Nach Berechnung des Brechungswinkel in A von N zu E wird der Tachymeter in A wieder aufgestellt und der tatsächliche Wert abgelesen. Aus der Differenz läßt sich die Querabweichung q berechnen.

3.3. Messprotokolle mit Verprobung

3.4. Auswertung der Beobachtungsdaten

Horizontalwinkelmessung

Siehe Messprotokoll

Vertikalwinkelmessung

Siehe Messprotokoll

Höhenindexfehler

n: Anzahl der Sätze

Rest siehe Messprotokoll

Längenmessung

Siehe Messprotokoll

3.5. Statistik

Horizotalwinkelmessung

Standardabweichung einer Messung:

n: Anzahl der Beobachtungen

d: Differenz der Satzmittel

d [mgon]	d² [mgon²]
-1,0	1
+1,0	1
+-0,05	0,0025
+-0,05	0,0025
-0,3	0,81
0,3	0,81
å d= 0	å d²= 3,625

Wenn eine Abweichung 0 beträgt (zwischen A und Punkt 2), so wird eine fiktive Standardabweichung von 0,00005 gon angenommen.

Standardabweichung aus Doppelbeobachtungen:

Vertikalwinkelmessung

Standardabweichung einer Messung

n: Anzahl der Beobachtungen

d: Differenz der Satzmittel

d [mgon]	d² [mgon²]
0	0
3	9
0,6	0,36
	å d²=9,36 mgon²

Standardabweichung aus Doppelbeobachtungen:

Längenmessung:

Vorgegebene Standardstreckenmessgenauigkeit:

m_s = ± (5mm+(5mm/km)× s)

s₁=23,943m ± 5,12mm

s₂=92,814m ± 5,46mm

s₃=48,249m ± 5,24mm

db₁=db₂= db₃= 0,00039 gon

Standardabweichung der Koordinatenunterschiede nach dem Varianzfortpflanzungsgesetz:

Errechnung von Y_E:

Y_E = Y_A + s₁ sin (t₀+b₁-200) + s₂ sin (t₀+b₁+b₂-400 ) + s₃ sin (t₀+b₁+b₂+b₃-600)

dY_E=

sin (t₀+b₁-200) ds₁

+ sin (t₀+b₁+b₂-400 ) ds₂

+ sin (t₀+b₁+b₂+b₃-600 ) ds₃

+ (s₁ cos(t₀+b₁-200) + s₂ cos (t₀+b₁+b₂-400 ) + s₃ cos (t₀+b₁+b₂+b₃-600) ) db₁/r

+ (s₂ cos (t₀+b₁+b₂-400 ) + s3 cos (t₀+b₁+b₂+b₃-600) ) * db₂/r

+ (s₃ cos (t₀+b₁+b₂+b₃-600) ) db₃/r

dY_E=

[ sin² (t₀+b₁-200)(ds₁)²

+ sin² (t₀+b₁+b₂-400 )(ds₂)²

+ sin² (t₀+b₁+b₂+b₃-600 )(ds₃)²

+ (s₁ * cos(t₀+b₁-200) + s₂ cos (t₀+b₁+b₂-400 ) + s₃ cos (t₀+b₁+b₂+b₃-600) )² (db₁/r)²

+ (s₂ cos (t₀+b₁+b₂-400 ) + s3 cos (t₀+b₁+b₂+b₃-600) )² (db₂/r)²

+ (s₃ cos (t₀+b₁+b₂+b₃-600) )² (db₃/r)² ]^0.5

Einsetzten ergibt:

d Y_E = 0,0073 m = 7,3 mm

Errechnung von X_E:

XE = XA + s₁ cos(t₀+b₁-200) + s₂ cos (t₀+b₁+b₂-400 ) + s₃ cos (t₀+b₁+b₂+b₃-600)

dX_E=

cos (t₀+b₁-200) ds₁

+ cos (t₀+b₁+b₂-400 ) ds₂

+ cos (t₀+b₁+b₂+b₃-600 ) ds₃

+ (s₁ sin(t₀+b₁-200) + s₂ cos (t₀+b₁+b₂-400 ) + s₃ cos (t₀+b₁+b₂+b₃-600) ) db₁/r

+ (s₂ sin (t₀+b₁+b₂-400 ) + s3 cos (t₀+b₁+b₂+b₃-600) ) db₂/r

+ (s₃ sin (t₀+b₁+b₂+b₃-600) ) db₃/r

dX_E=

[ cos² (t₀+b₁-200) (ds₁)²

+ cos² (t₀+b₁+b₂-400 ) (ds₂)²

+ cos² (t₀+b₁+b₂+b₃-600 ) (ds₃)²

+ (s₁ sin (t₀+b₁-200) + s₂ sin (t₀+b₁+b₂-400 ) + s₃ sin (t₀+b₁+b₂+b₃-600) )² (db₁/r)²

+ (s₂ sin (t₀+b₁+b₂-400 ) + s3 sin (t₀+b₁+b₂+b₃-600) )² (db₂/r)²

+ (s₃ sin (t₀+b₁+b₂+b₃-600) )² (db₃/r)² ]^0.5

Einsetzten ergibt:

d X_E = 0,0056 m = 5,6 mm

b _soll = a -(t0-200) = 68,7181 gon - 143,9200 gon + 200gon=124,7981 gon

b _ist = 124,794 gon

à fiktive Querabweichung d b =0,004 gon = 4 mgon

r = 63,6620 gon

3.6. Zusammenfassung der Ergebnisse und beurteilende Stellungnahme

Da es sich um einen offenen Polygonzug handelte, wurden die Koordinaten durch den direkt von PA zu PE gemessenen Winkel b überprüft.

Erfreulicherweise konnten alle Toleranzen eingehalten werden, so dass wir unsere Messung durchaus als realistisch bezeichnen können.

Ob die Koordinaten des Endpunktes stimmen, kann man nicht sagen, da witterungsbedingt weder der Kirchturm noch die Antennen auf dem Kamin zu erkennen waren, so dass wir uns mit einer Eisenstangen, die grob in der Richtung der Kirche stand, begnügen mussten.