Fourier-Reihen

Allgemeines

Konvergenz

Symmetrie

Als Fourier-Reihen bezeichnet man die beste Approximation einer periodischen Funktion im quadratischen Mittel (d.h. die beste Annäherung einer Funktion durch eine trigonometrische Reihe). Das Quadratische Mittel ist eine mathematische Norm (die sogenannte 2-er Norm). Mit Hilfe dieser 2-Norm entsteht ein normierter Vektorraum, mit dem sich der Abstand zwischen zwei Funktionen messen lässt. Geometrisch ist die 2-Norm die Wurzel aus dem Quadrat der zwischen zwei Funktionen eingeschlossenen Fläche:

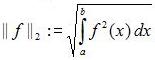
Insbesondere bei 2-π periodischen Funktionen läßt sich die Fourierreihe wie folgt formulieren:

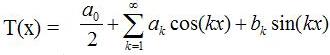
wobei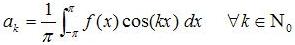und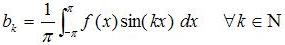

Dieses Bildungsgesetz kommt natürlich nicht von irgendwo her, sondern läßt sich mit Hilfe eines Orthonormalsystems (ONS) herleiten. Ein ONS wird aus Funktionen gebildet die paarweise senkrecht aufeinanderstehen und auf ihre Länge normiert sind. Dies ist bei Funktionen nicht mehr geometrisch vorstellbar, jedoch gilt das gleiche im n-dimensionalen Vektorraum. Auch Vektoren können ein ONS bilden (stehen normal zueinander und besitzen die Länge 1), die dann einen Unterraum der betrachteten Dimension aufspannen.

Aus den folgenden drei Funktionen die im Intervall [-π,π] ein solches ONS bilden leitet sich die Formel für 2π-periodische Fourierreihen her:

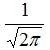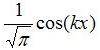und und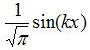

Man kann sich mit Hilfe des Skalarproduktes leicht davon überzeugen das sie normal zueinander stehen (ausführlicher Beweis siehe Burg-Haf-Wille / Mathematik für Ingenieure).

Konvergenz

Es stellt sich noch die Frage in welchen Fällen die Fourierreihe gegen die vorgegeben Funktion konvergiert. Man kann in einem ziemlich aufwändigem Beweis zeigen das punktweise Konvergenz genau da vorliegt wo die Ursprungsfunktion stetig ist. An Unstetigkeitsstellen dagegen konvergiert die unendliche Reihe gegen den Mittelwert aus rechts- und linksseitigem Grenzwert. Wie man sich leicht vorstellen kann treten solche Unstetigkeitsstellen vorwiegend an den Periodenübergängen auf. Es gilt also:

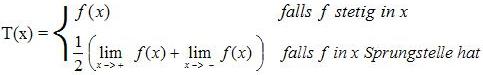
Hinsichtlich der gleichmäßigen Konvergenz gilt etwas ganz analoges. In abgeschlossenen Stetigkeitsintervallen liegt immer gleichmäßige Konvergenz vor. Jedoch an Sprungstellen wird diese verletzt. Dies äußert sich graphisch durch das sogenannte Gibbsche Phänomen. Danach treten an den Unstetigkeitsstellen starke Überschwinger auf. Diese werden auch bei zunehmenden Grad nicht kleiner sondern rücken nur näher an die Sprungstelle heran (siehe weiter unten Skizze einer nicht stetigen Funktion).
Mit dieser Eigenschaft der gleichmäßigen Konvergenz leitet sich nun ganz automatisch eine Aussage über das gliedweise Integrieren von Fourierreihen ab. Denn überall dort wo wir gleichmäßige Konvergenz haben ist die Ausgangsfunktion stetig und diese beiden Eigenschaften sind, wie wir wissen, die Vorraussetzungen für das gliedweise Integrieren. An den Sprungstellen (nur punktweise Konvergenz) trennen wir das Integral auf und erhalten somit auf dem ganzen Periodenintervall Integrierbarkeit.

Symmetrieeigenschaften

Die Fourierkoeffizienten a_k und b_k lassen sich bei bestimmten Symmetrien noch vereinfachen:

	Bei ungeraden Funktionen ist der ak-Integerant ungerade und der bk-Integrant gerade. Mit den vorgegebenen symmetrischen Integralgrenzen folgt:
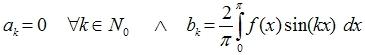	Bei geraden Funktionen ist der ak-Integerant gerade und der bk-Integrant ungerade. Da auch hier symmetrische Intervalle zum Ursprung vorliegen über die integriert wird, ergibt sich:
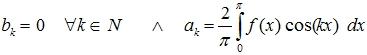	Gilt f(t) = f(t+T/2) und ist die Funktion damit nicht nur in T periodisch sondern auch in der halben Periode T/2, so nennt man dies "Vollwellensymmetrie". Bei der hier entstehenden Fourierreihe treten deshalb nur geradzahlige Vielfache der Grundschwingung auf (geradzahlige Harmonische). Wie bei den geraden Funktionen gilt auch hier, dass das Integeral von [-π,0] den gleichen Inhalt liefert wie [0,π]:

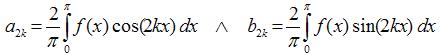Beispiel einer Fourierreihe