![]() ,
,
![]() ,
,
![]() .
.
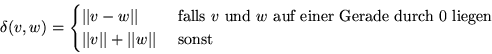
Zeige, dass ![]() tatsächlich eine Metrik ist.
tatsächlich eine Metrik ist.
Y ist genau dann offen, wenn ![]() und
genau dann abgeschlossen, wenn
und
genau dann abgeschlossen, wenn ![]() .
.
Zeige:
![]() ist auch kompakt.
ist auch kompakt.
Zeige:
Die durch ![]() gegebene
Abbildung
gegebene
Abbildung ![]() ist stetig.
ist stetig.
Zeige, dass F stetig ist.
PD Dr. Jörg Winkelmann
![]() ,
,
![]() ,
,
![]() .
.
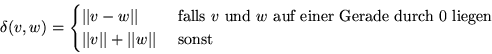
Zeige, dass ![]() tatsächlich eine Metrik ist.
tatsächlich eine Metrik ist.
Y ist genau dann offen, wenn ![]() und
genau dann abgeschlossen, wenn
und
genau dann abgeschlossen, wenn ![]() .
.
Zeige:
![]() ist auch kompakt.
ist auch kompakt.
Zeige:
Die durch ![]() gegebene
Abbildung
gegebene
Abbildung ![]() ist stetig.
ist stetig.
Zeige, dass F stetig ist.