Folgt daraus, dass auch ![]() konvergent ist?
konvergent ist?
Für alle ![]() , c>1 gilt:
, c>1 gilt: ![]() für
für 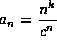 .
.
(Tip:
Zeige zuerst ![]() und
dann
und
dann ![]() .)
.)
- (*) 6.
-
Zeige:
Jede Folge besitzt eine monotone Teilfolge.
Joerg Winkelmann
Thu Nov 18 22:56:28 MET 1999
PD Dr. Jörg Winkelmann
Folgt daraus, dass auch ![]() konvergent ist?
konvergent ist?
Für alle ![]() , c>1 gilt:
, c>1 gilt: ![]() für
für 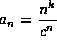 .
.
(Tip:
Zeige zuerst ![]() und
dann
und
dann ![]() .)
.)